MEDIDAS DE TENDENCIA CENTRAL, POSICIÓN Y DISPERSIÓN (TEMA 8)

Buenos días a todos! En esta entrada vamos a dar un paso más en el campo de la estadística. Hablaremos de las medidas de tendencia central, posición y dispersión.

Lo primero que quiero mostraros es cómo hacer un resumen numérico de un serie estadística: se trata de otra alternativa a la hora de agrupar los datos estadísticos, además de las tablas y gráficos. Debemos tener en cuenta que solo se aplican a variables cuantitativas continuas (edad, peso, talla..)

Existen tres medidas estadísticas:

• Medidas de posición: nos muestran la magnitud, tamaño o posición de los datos observados (estos están ordenados de menor a mayor).
• Medidas de tendencia central: muestran el comportamiento central de los sujetos de estudio.
• Medidas de dispersión o variabilidad: muestran la heterogeneidad que puedan compartir los sujetos, es decir, sus diferencias.

MEDIDAS DE TENDENCIA CENTRAL:

Media aritmética: se calcula para variables cuantitativas y se trata del centro de gravedad de nuestros datos. Su fórmula es:

Es la suma de todos los valores de la variable observada entre el total de observaciones.

Cuando los datos están agrupados (dos intervalos), para calcular la media utilizamos como valor de referencia de cada intervalo su marca de clase: se calcula una media aritmética ponderada que se calcula sumando la marca de clase por la frecuencia absoluta, entre n.

Recordemos como se calcula la marca de clase:

x= Ʃm_c (marca de clase) x fi (frecuencia absoluta) /n (multiplicamos la marca de clase por la frecuencia absoluta y vamos sumando, luego dividimos entre el número de sujetos)

Mediana: es el valor de la observación en el que un 50% de los datos es menor y el otro 50% es mayor.

• Si el número de observaciones es impar: n +1/2 Ejemplo: si son 75, pues 76 entre 2 = 38, la mediana seria la edad que tiene el sujeto 38.
• Si el número de observaciones es par: n/2  

Recordemos que n = Número de Observaciones de nuestro estudio.

Moda: es el valor con mayor frecuencia, es decir, el que más veces se repite.

• Existen dos valores que más se repiten: moda Bimodal.
• Existen más de dos valores que más se repiten: moda Multimodal.

MEDIDAS DE POSICIÓN o CUANTILES:

Se calculan para variables cuantitativas, se tiene en cuenta la posición de los valores en la muestra.

• Percentiles: dividen la muestra ordenada en 100 partes. El valor del P₅₀ corresponde al valor de la mediana.
• Deciles: dividen la muestra ordenada en 10 partes. El valor del D₅ corresponde al valor de la mediana y, por tanto, al del P₅₀.
• Cuartil: dividen la muestra ordenada en 4 partes. El Q₄, cuarto cuartil indica el valor mayor que se alcanza en la serie numérica.

    MEDIDAS DE DISPERSIÓN:

      

    Rango o recorrido: diferencia entre el mayor y el menor valor de la muestra  lX_n-X₁l (valor absoluto).

     Desviación media: media aritmética de las distancias de cada observación con respecto a la media.

Desviación típica o estándar: nos indica el error que cometemos si representamos una muestra guiándonos solo por su media.

Varianza: expresa la misma información, pero en valores al cuadrado.

DISTRIBUCIONES NORMALES

Se llama distribución normal a una de las distribuciones de probabilidad de variable continua que con más frecuencia aparece en fenómenos reales.

La gráfica de su función de densidad tiene una forma acampanada y es simétrica respecto de los valores posición central (media, mediana y moda, que coinciden en estas distribuciones).

Esta curva se conoce como campana de Gauss

ASIMETRIAS Y CURTOSIS

La asimetria es el lado opuesto de nuestras medidas estadísticas.

• Coeficiente de asimetría de una variable: grado de asimetría de la distribución de sus datos en torno a su media. Si es más asimétrica indica que los valores son más diferentes entre sí.

Los resultados pueden ser:

• g1=0 (distribución simétrica; existe la misma concentración de valores a la derecha y a la izquierda de la media).
• g1>0 (distribución asimétrica positiva; existe mayor concentración de valores  a la derecha de la media que a su izquierda).
• g1<0 (distribución asimétrica negativa; existe mayor concentración de valores a la izquierda de la media que a su derecha).

Curtosis o apuntamiento de la curva: sirve para medir el grado de concentración de los valores que toma en torno a su media. Mientras más datos se acumulen, más apuntada será la curva.

Los resultados pueden ser:

• g2=0 (distribución mesocúrtica o normal). Presenta un grado de concentración medio alrededor de los valores centrales de la variable (el mismo que presenta una distribución normal).
•  g2>0 (distribución leptocúrtica). Presenta un elevado grado de concentración alrededor de los valores centrales de la variable.
• g2<0 (distribución platicúrtica). Presenta un reducido grado de concentración alrededor de los valores centrales de la variable.

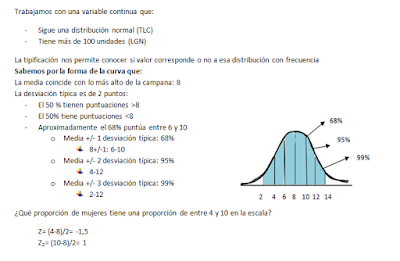
Por último, os dejo un ejemplo sobre la tipificación de los valores y su relación con la campana de Gauss:

Espero que os sirva de ayuda!!